数学学院张小红教授团队在国际权威期刊发表5篇高水平论文

近来，我校特聘教授张小红团队在不确定性数学与数据智能方向取得多项重要进展，连续在国际权威期刊Information Sciences（SCI一区TOP，影响因子8.233）、Expert Systems with Applications（SCI一区TOP，影响因子8.665）、Fuzzy Sets and Systems（SCI一区TOP，影响因子4.462）发表论文5篇。这些论文均以yl12311线路检测为第一完成单位，张小红教授、于鹏副教授、张会博士、刘慧博士、师资博士后王敬前、在读博士生王梅、在读硕士研究生宋虎雄、尚姣妍、梁嵘、李梦园等分别为论文第一作者、通讯作者或主要作者。论文合作者中还包括巴西著名学者Benjamin Bedregal教授、张海教授（西北大学统计系主任，陕西省统计学学会副理事长）、梁勇（鹏城实验室研究员，中国工业与应用数学学会理事）、代建华教授（湖南师范大学信息科学与工程学院院长）、詹建明教授（湖北民族大学、ESI全球高被引科学家）等。

文章列表及简介如下：

1. Xiaohong Zhang, Mei Wang, Benjamin Bedregal, et al., Semi-overlap functions and novel fuzzy reasoning algorithms with applications,Information Sciences,2022, 614: 104-122.

   本文发展了著名学者H. Bustince（IEEEFellow）创建的重叠函数理论，首次引入半重叠函数的概念，系统研究了半重叠函数的性质和构造方法；基于半重叠函数及其诱导的剩余蕴涵，给出了解决模糊推理FMP问题的QIP方法；借助半重叠函数和QIP方法，提出了一种新的数据分类算法—SO5I-FRC算法，数据实验表明，SO5I-FRC算法比国外学者提出的FARC-HD算法的分类准确率高。

2. Xiaohong Zhang, Jiaoyan Shang, Jingqian Wang, Multi-granulation fuzzy rough sets based on overlap functions with a new approach to MAGDM,Information Sciences,2023, 622: 536-559.

   本文首次借助n-维重叠函数建立了两种多粒度模糊粗糙集模型，并将其应用于多属性群体决策问题。首先，利用幂等n-维重叠函数建立乐观和悲观的多粒度模糊粗糙集模型，这些新模型充分保留了传统粗糙集模型的重要特性。其次，结合TOPSIS方法，提出了基于所建模型的多属性群体决策方法。最后，与现有决策方法进行比较，结果表明所提方法更有效。

3. Jingqian Wang, Xiaohong Zhang, Jianhua Dai, Jianming Zhan, TI-fuzzy neighborhood measures and generalized Choquet integrals for granular structure reduction and decision making, Fuzzy Sets and Systems, Available online 3 April 2023, DOI: 10.1016/j.fss.2023.03.015.

   本文提出了TI-模糊邻域测度，并将其用于模糊覆盖近似空间中的粒结构约简和决策问题。首先，利用t-模“T”及其诱导的剩余蕴含“I_T”提出了四对TI -模糊邻域测度，用于代替已有粒计算中的粗糙近似算子。然后，提出了一种利用TI -模糊邻域测度来实现粒结构约简的方法。其次，构造了四对基于TI -模糊邻域测度的广义Choquet积分，将所构造的广义Choquet积分与模糊PROMETHEE方法相结合，提出了一种新的智能决策方法。最后，通过公开数据集验证了所提方法的可行性和有效性。

4. Hui Zhang, Shoujiang Li, Yong Liang, et al., UAMPnet: Unrolled approximate message passing network for nonconvex regularization, Expert Systems with Applications, 2023, 213, Part C, 119220. DOI: 10.1016/j.eswa.2022.119220.

   本工作借助深度学习的性能优势研究了两种流行的非凸正则化方法的高效求解算法，提出了两种新颖的深度展开网络并给出了收敛性分析。此外，通过稀疏信号重建和5G无线通信实验验证了所提深度网络的有效性。

5. Hu Xiong Song, Peng Yu, Hui Liu, From pre-(quasi-) grouping functions to directional monotonic fuzzy implications, Fuzzy Sets and Systems, Available online 2 December 2022, DOI: 10.1016/j.fss.2022.12.001.

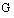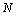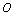   本文将(拟-)分组函数中的单调性拓展为方向单调性，提出并研究了预-(拟-)分组函数的概念与性质，给出了预-(拟-)分组函数的几种构造方法。同时，基于预-(拟-)分组函数、模糊否定和重叠函数，构造了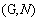-方向单调模糊蕴涵和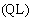-方向单调算子，并对以上方向单调算子进行了刻画。

   （核稿：李剑 编辑：雷超）